Structural Equation Modeling (SEM) is an extension of the General Linear Model (GLM) that enables a researcher to test a set of regression equations simultaneously. SEM software can test traditional models, but it also permits examination of more complex relationships and models, such as confirmatory factor analysis and time series analyses.
The basic approach in performing an SEM analysis is as follows:
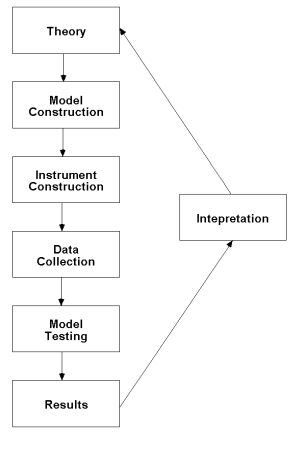
The researcher first specifies a model based on theory, then determines how to measure constructs, collects data, and then inputs the data into the SEM software package. The package fits the data to the specified model and produces the results, which include overall model fit statistics and parameter estimates.
The input to the analysis is usually a covariance matrix of measured variables such as survey item scores, though sometimes matrices of correlations or matrices of covariances and means are used. In practice, the data analyst usually supplies SEM programs with raw data, and the programs convert these data into covariances and means for its own use.
Useful links: How to calculate covariance in a spreadsheet?
How to find Covariance between two variables using R?
The model consists of a set of relationships among the measured variables. These relationships are then expressed as restrictions on the total set of possible relationships.
The results feature overall indexes of model fit as well as parameter estimates, standard errors, and test statistics for each free parameter in the model.


