A derivative is one of the main and well-known types of calculus. Calculus is the mathematical technique used to study functions for calculating the area and slope of the tangent line according to the independent variables of the functions.
In this post, we will learn the definition and rules of differentiation along with a lot of examples to learn how to evaluate its advanced problems using rules.
What is differential in calculus?
The differential is the main type of calculus along with the integral. Differential calculus is a process of finding the instantaneous rate of change of a function with respect to the independent variable of the function.
The process of finding the derivative of the function is also known as differentiation. It is used to find the slope of the tangent line. It is helpful in evaluating the original function in the form of a differential function.
The slope of the tangent can be evaluated with the help of the limit as the given function should be added an arbitrary point “h” and subtract it from the original function over “h” as the limit approaches zero is said to be the differential of the function using first principle method.
Slope of tangent = f’(x) = limh→0 f(x + h) – f(x) / h
The above formula is used for finding the differential of the function with the help of the limit and is known as the first principle method. This method will provide the accurate result of the differentiated function in an easy way.
There is another way to find the differential of the function which is with the help of the rules of differentiation. Now we’ll discuss the rules of differentiation.
Rule of differential calculus
There are various kinds of rules of differential calculus. Below are a few well-known rules of differentiation.
1. Constant Rule
d/dy [C] = 0
The “C” is for any constant integer, function, or expression. This means the differential of any constant term is always zero.
2. Constant Function Rule
d/dy [C f(y)] = C d/dy [f(y)]
3. Power Rule
d/dy [ym] = m ym-1 d/dy [y]
4. Sum Rule
d/dy [f(y) + g(y)] = d/dy [f(y)] + d/dy [g(y)]
The sum rule is used to write the differential notation with each term of the function after the plus sign.
5. Difference Rule
d/dy [f(y) – g(y)] = d/dy [f(y)] – d/dy [g(y)]
The difference rule is used to write the differential notation with each term of the function after the minus sign.
6. Quotient Rule
d/dy [f(y) / g(y)] = 1/[g(y)]2 [g(y) d/dy [f(y)] – f(y) d/dy [g(y)]
7. Product Rule
d/dy [f(y) * g(y)] = g(y) d/dy [f(y)] + f(y) d/dy [g(y)]
8. Trigonometry formulas
Here are some well-known formulas of the trigonometric functions
| d/dy [cos(y)] | -sin(y) |
| d/dy [sin(y)] | Cos(y) |
| d/dy [tan(y)] | Sec2(y) |
| d/dy [cot(y)] | -cosec2(y) |
| d/dy [sec(y)] | Sec(y) tan(y) |
| d/dy [cosec(y)] | -cosec(y) cot(y) |
| d/dy [cos2(y)] | -2cos(y) sin(y) |
| d/dy [sin2(y)] | 2sin(y) cos(y) |
How to solve advanced problems of differential calculus?
The advanced problems of differential calculus can be solved with the help of rules and formulas. Let us take a look at how to evaluate the problems of differential calculus.
Example 1
Evaluate the differential of the given function with respect to “y”.
f(y) = 3y3 – 2y2 + 4sin2(y) + 5sec(y) + cos(y)
Solution
Manual method
Step 1: First of all, write the given function along with the differential notation.
f(y) = 3y3 – 2y2 + 4sin2(y) + 5sec(y) + cos(y)
d/dy [f(y)] = d/dy [3y3 – 2y2 + 4sin2(y) + 5sec(y) + cos(y)]
Step 2: Now write the notation of differential with each term of the above expression with the help of the sum and difference rules of differentiation.
d/dy [3y3 – 2y2 + 4sin2(y) + 5sec(y) + cos(y)] = d/dy [3y3] – d/dy [2y2] + d/dy [4sin2(y)] + d/dy [5sec(y)] + d/dy [cos(y)]
Step 3: Now write the above expression by applying the constant function rule.
d/dy [3y3 – 2y2 + 4sin2(y) + 5sec(y) + cos(y)] = 3d/dy [y3] – 2d/dy [y2] + 4d/dy [sin2(y)] + 5d/dy [sec(y)] + d/dy [cos(y)]
Step 4: Now use the power rule and trigonometric formulas to the above expression to find the differential of the given function.
d/dy [3y3 – 2y2 + 4sin2(y) + 5sec(y) + cos(y)] = 3 [3 y3-1] – 2 [2 y2-1] + 4 [2 sin2-1(y) [sin(y)]] + 5 [sec(y) tan(y)] + [-sin(y)]
d/dy [3y3 – 2y2 + 4sin2(y) + 5sec(y) + cos(y)] = 3 [3 y2] – 2 [2 y1] + 4 [2 sin1(y) d/dy [sin(y)]] + 5 [sec(y) tan(y)] + [-sin(y)]
d/dy [3y3 – 2y2 + 4sin2(y) + 5sec(y) + cos(y)] = 3 [3y2] – 2 [2y] + 4 [2sin(y) [cos(y)]] + 5 [sec(y) tan(y)] + [-sin(y)]
d/dy [3y3 – 2y2 + 4sin2(y) + 5sec(y) + cos(y)] = 9y2 – 4y + 8sin(y) cos(y) + 5sec(y) tan(y)] – sin(y)
By using a differential calculator
As the advanced problems of differential calculus take a larger number of steps to differentiate a function. A differential calculator by MeraCalculator is a helpful online source to evaluate the above problem to avoid these calculations.
Step 1: Enter the function and select the variable.
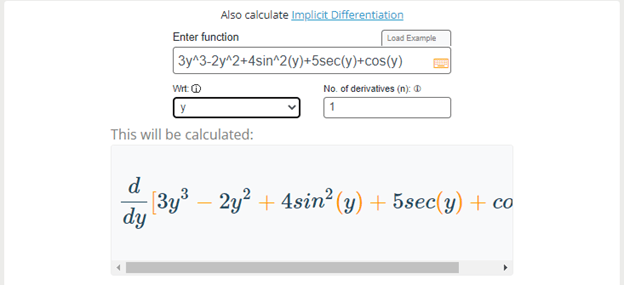
Step 2: Hit the calculate button.
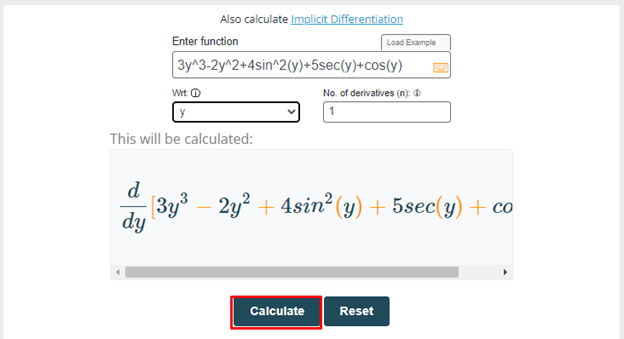
Step 3: The step-by-step solution will come in a couple of a second. Press show more for viewing the steps.
Example 2
Find the differential of the given function with respect to “u”.
f(u) = 5u5 + 3u2 – 2u3 + 5cosec(u) + 12sin(u) + 2
Solution
Step 1: First of all, write the given function along with the differential notation.
f(u) = 5u5 + 3u2 – 2u3 + 5cosec(u) + 12sin(u) + 2
d/du [f(u)] = d/du [5u5 + 3u2 – 2u3 + 5cosec(u) + 12sin(u) + 2]
Step 2: Now write the notation of differential with each term of the above expression with the help of the sum and difference rules of differentiation.
d/du [5u5 + 3u2 – 2u3 + 5cosec(u) + 12sin(u) + 2] = d/du [5u5] + d/du [3u2] – d/du [2u3] + d/du [5cosec(u)] + d/du [12sin(u)] + d/du [2]
Step 3: Now write the above expression by applying the constant function rule.
d/du [5u5 + 3u2 – 2u3 + 5cosec(u) + 12sin(u) + 2] = 5d/du [u5] + 3d/du [u2] – 2d/du [u3] + 5d/du [cosec(u)] + 12d/du [sin(u)] + d/du [2]
Step 4: Now use the power rule, constant rule, and trigonometric formulas to the above expression to find the differential of the given function.
d/du [5u5 + 3u2 – 2u3 + 5cosec(u) + 12sin(u) + 2] = 5 [5 u5-1] + 3 [2 u2-1] – 2 [3 u3-1] + 5 [-cosec(u) cot(u)] + 12 [cos(u)] + [0]
d/du [5u5 + 3u2 – 2u3 + 5cosec(u) + 12sin(u) + 2] = 5 [5 u4] + 3 [2 u1] – 2 [3 u2] + 5 [-cosec(u) cot(u)] + 12 [cos(u)] + [0]
d/du [5u5 + 3u2 – 2u3 + 5cosec(u) + 12sin(u) + 2] = 5 [5u4] + 3 [2u] – 2 [3u2] + 5 [-cosec(u) cot(u)] + 12 [cos(u)]
d/du [5u5 + 3u2 – 2u3 + 5cosec(u) + 12sin(u) + 2] = 25u4 + 6u – 6u2 – 5cosec(u) cot(u) + 12cos(u)
Conclusion
In this article, we have discussed the term differential calculus and its rules. We also discussed the advanced examples of differential calculus by using a manual method and using a calculator. You can take assistance from this post to evaluate the problems of derivatives or you can try an online calculator for better results.
