Limit is a well-known and frequently used technique in calculus for defining the term integral, continuity, and differentiation. In integral, the limits are used to find the area under the curve with the help of boundary values.
In continuity, the term limit is used to check whether the function is true or false. While in differentiation, the limit is used to differentiate the given function with the help of the first principle method. In this post, we’ll learn the definition, rules, and solved examples of limit calculus.
What is limit calculus?
In calculus, the limit is used to find the numerical value of the function at a particular point. The function f(t) at the particular point t approaches some value is said to be the limit of that function and mathematically it can be written as:
Limt→u f(t) = F(t) = L
Rules of limit calculus
There are several rules for calculating the limit of a function. Here are some rules of limit and a brief introduction with examples.
Power Rule of Limit Calculus
The power rule of limit calculus is used to determine the limit of the exponent functions by applying the specific point to the function and taking the exponent of that numerical value. The expression of power rule of Limit Calculus is:
Limt→u f(t)n = [Limt→u f(t)]n
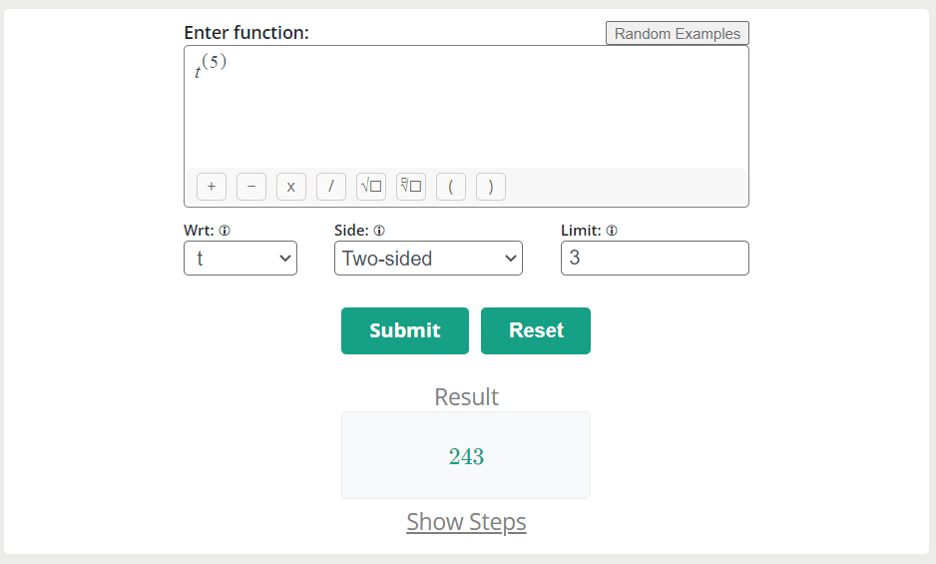
For example, if the given function is t5 and the specific point of the function is 3:
Solution
Step 1: Take the function and apply the limit value.
Limt→u f(t)n = Limt→3 t5
Step 2: Apply the power rule of limit calculus
Limt→3 t5 = [Limt→3 t]5
Limt→3 t5 = [3]5
Limt→3 t5 = [3 x 3 x 3 x 3 x 3]
Limt→3 t5 = [243]
You can also try a limit calculator with steps to evaluate the limit problems without involving into calculations.
Sum Rule of Limit Calculus
The sum rule of limit calculus is used when two or more addition terms are present in a function and it will allow you to apply the limit notation to each term of the function separately with the sum sign.
Limt→u [f(t) + g(t)] = Limt→u [f(t)] + Limt→u [g(t)]
For example, if the given function is t5 + t3 and the specific point of the function is 2:
Solution
Step 1: Take the function and apply the limit value.
Limt→u [f(t) + g(t)] = Limt→2 [t5 + t3]
Step 2: Apply the sum rule of limit calculus
Limt→2 [t5 + t3] = Limt→2 [t5] + Limt→2 [t3]
Limt→2 [t5 + t3] = [Limt→2 t]5 + [Limt→2 t]3
Limt→2 [t5 + t3] = [2]5 + [2]3
Limt→2 [t5 + t3] = [2 x 2 x 2 x 2 x 2] + [2 x 2 x 2]
Limt→2 [t5 + t3] = [32] + [8]
Limt→2 [t5 + t3] = 40
Difference Rule of Limit Calculus
The difference rule of limit calculus is used when two or more subtraction terms are present in a function and it will allow you to apply the limit notation to each term of the function separately with the sum sign.
Limt→u [f(t) – g(t)] = Limt→u [f(t)] – Limt→u [g(t)]
For example, if the given function is t5 – t3 and the specific point of the function is 2:
Solution
Step 1: Take the function and apply the limit value.
Limt→u [f(t) – g(t)] = Limt→2 [t5 – t3]
Step 2: Apply the difference rule of limit calculus
Limt→2 [t5 – t3] = Limt→2 [t5] – Limt→2 [t3]
Limt→2 [t5 – t3] = [Limt→2 t]5 – [Limt→2 t]3
Limt→2 [t5 – t3] = [2]5 – [2]3
Limt→2 [t5 – t3] = [2 x 2 x 2 x 2 x 2] – [2 x 2 x 2]
Limt→2 [t5 – t3] = [32] – [8]
Limt→2 [t5 – t3] = 24
Constant Rule of Limit Calculus
The limit of a function is only applied when there is a function available according to the independent variable. If there is no function present, then the limit is not applied to it.
Limt→u [f(x)] = f(x)
For example, if the given function is x2 and the specific point of the function is 2:
Solution
Step 1: Take the function and apply the limit value.
Limt→u [f(t)] = Limt→2 [x2]
Step 2: apply the constant rule of limit calculus
Limt→2 [x2] = x2
L’hopital’s Rule of Limit Calculus
This rule is applied when a function makes an undefined form. This rule will take the derivative of the numerator and denominator to make the function defined.
Limt→u [f(t) / g(t)] = Limt→u [d/dt f(t)] / [d/dt (g(t))]
For example, if the given function is t2 – 1 / t – 1 and the specific point of the function is 1:
Solution
Step 1: Take the function and apply the limit value.
Limt→u [f(t) / g(t)] = Limt→1 [t2 – 1 / t – 1]
Step 2: Apply the quotient rule of limit calculus
Limt→1 [t2 – 1 / t – 1] = Limt→1 [t2] – Limt→1 [1] / Limt→1 [t] – Limt→1 [1]
Limt→1 [t2 – 1 / t – 1] = [12] – [1] / [1] – [1]
Limt→1 [t2 – 1 / t – 1] = [1 – 1] / [1 – 1]
Limt→1 [t2 – 1 / t – 1] = 0 / 0
Step 3: Now apply the L’hopital rule of limit calculus.
Limt→1 [t2 – 1 / t – 1] = Limt→1 [d/dt (t2 – 1) / d/dt(t – 1)]
Limt→1 [t2 – 1 / t – 1] = Limt→1 [2t – 0) / (1 – 0)]
Limt→1 [t2 – 1 / t – 1] = Limt→1 [2t / 1]
Limt→1 [t2 – 1 / t – 1] = Limt→1 [2t]
Limt→1 [t2 – 1 / t – 1] = 2(1)
Limt→1 [t2 – 1 / t – 1] = 2
Product Rule of Limit Calculus
The product rule of limit calculus is used when two or more subtraction terms are present in a function and it will allow you to apply the limit notation to each term of the function separately with the product sign.
Limt→u [f(t) * g(t)] = Limt→u [f(t)] * Limt→u [g(t)]
For example, if the given function is 3t2 * 2t and the specific point of the function is 2:
Solution
Step 1: Take the function and apply the limit value.
Limt→u [f(t) * g(t)] = Limt→2 [3t2 * 2t]
Step 2: Apply the product rule of limit calculus
Limt→2 [3t2 * 2t] = Limt→2 [3t2] * Limt→2 [2t]
Limt→2 [3t2 * 2t] = 3Limt→2 [t2] * 2Limt→2 [t]
Limt→2 [3t2 * 2t] = 3 [2]2 * 2 [2]
Limt→2 [3t2 * 2t] = 3 [2 x 2] * 2 [2]
Limt→2 [3t2 * 2t] = 3 [4] * 2 [2]
Limt→2 [3t2 * 2t] = 12 * 4
Limt→2 [3t2 * 2t] = 48
Quotient Rule of Limit Calculus
The quotient rule of limit calculus is used when two or more subtraction terms are present in a function and it will allow you to apply the limit notation to each term of the function separately with the quotient sign.
Limt→u [f(t) / g(t)] = Limt→u [f(t)] / Limt→u [g(t)]
For example, if the given function is 15t / 2t2 and the specific point of the function is 3:
Solution
Step 1: Take the function and apply the limit value.
Limt→u [f(t) / g(t)] = Limt→3 [15t / 2t2]
Step 2: Apply the quotient rule of limit calculus
Limt→3 [15t / 2t2] = Limt→3 [15t] / Limt→3 [2t2]
Limt→3 [15t / 2t2] = 15Limt→3 [t] / 2Limt→3 [t2]
Limt→3 [15t / 2t2] = 15 [3] / 2 [32]
Limt→3 [15t / 2t2] = 15 [3] / 2 [3 x 3]
Limt→3 [15t / 2t2] = 15 [3] / 2 [9]
Limt→3 [15t / 2t2] = 45 / 18
Limt→3 [15t / 2t2] = 2.5
Conclusion
The limit in calculus can be evaluated with the help of its rules easily and quickly. You can grab all the basics of limit calculus and its rules from this post. We have explained the rules with solved examples and general expressions.
